ある音群を含むメジャースケールの見つけ方について

メジャースケールの成り立ちをそれらしく説明する方法はおそらく何通りもあり、そのうちどれが一番妥当か、などという議論にはそこまで意味はないと思いますが、そのうちの一つとして、「完全五度を6回くりかえしてできる音列（の並び替え）」というとらえ方があると思います。


すなわち、たとえばFの音から順番に完全五度ずつ上昇していくと、

F→C→G→D→A→E→B→...

という風になり、これを途中でやめずに続ければちょうど12回目でFに戻るわけですが、Bでやめておけば、ここまでに現れた7つの音がCメジャースケールを成します。


5度圏の中に図として表せば以下の通りです。

図のピンク色の部分がCメジャースケールです。


このように捉えておくと、ある和音なり音群があったとき、それを含むメジャースケールがどのくらい存在するか、ということの判定が直感的になります。

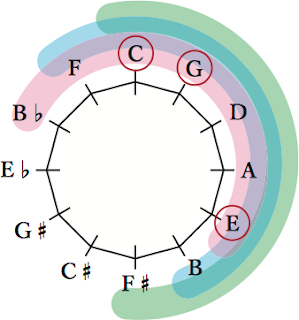
たとえば、Cのメジャートライアド（C,E,G）があったとすると、それを五度圏の中に表し、

上で見た、「連続する7音」でCとGとEを含むものを考えると、下の図の（ピンクと水色と緑の）3種類になります。

それらはつまり、FメジャースケールとCメジャースケールとGメジャースケールです。


この考え方はいろいろな応用ができると思います。たとえば、メロディに和音を付けたいとき、そのメロディに対して当てはめられるコードは何か考えるときなどです。



また、完全五度ずつ上昇していく音列を、（倍音列を根拠にしたりなどして）「ルート」から「テンションノート」へのなだらかな移行と捉えると、ある音や和音に対して、それが「低い」位置にあるようなスケール、「高い」位置にあるようなスケールを考えることもできます。

つまり、たとえばCメジャースケールを、FリディアンのようにFを一番下に持ってきて、C,G,D,...と進んでいくほどに、「アッパーストラクチャー」とか「テンションノート」とかのような、上部の構造になっていく、と考えることにします。上の5度圏の図では時計回りに進むほど上がっていくということです。

すると、上の例と同じく、Cのメジャートライアドがあったとき、それが一番「高い」位置、「アッパーストラクチャー」の位置にくるようなメジャースケールは、上の図のピンクのもの（Fメジャースケール=Bbリディアンスケール）であるし、一番「低い」位置にくるものは、上の図の緑のもの（Gメジャースケール=Cリディアンスケール）です。


この考え方はメロディへの和音の付け方への一つの尺度として機能しうると思います。



最後に、このようなとらえ方は、メジャースケール（=アイオニアン）と、その転回形、つまりいわゆる7種類の教会旋法には応用ができますが、ハーモニックマイナーやメロディックマイナーなどの場合は、完全五度ずつの上昇の結果として生まれるスケールではないので、このような単純な議論はできません。
また、7音音階ではなければ、たとえば「メジャーペンタ」「マイナーペンタ」などは完全五度を積み上げることで作られるので、同様に考えることができます。

ある音群を含むメジャースケールがどのくらいあるのか、ということについても記事にしたいと思います。